Everyday is somebody’s birthday. Image from wishbirthday.org
by George Taniwaki
I have a Facebook friend whose birthdate was listed as January 1. When I saw this, I thought, “That can’t be true. Nobody is born on January 1.” But later, I realized that isn’t true. People are born on every day of the year. So just how likely is it that my friend’s birthdate in January 1?
Distribution of actual birthdates
If birthdates are distributed evenly, then every day should have the same number of births. Even if births are distributed evenly on all days, not every birthdate will have the same number of births because of leap years. Thus, except February 29, each day has a probability of 1 out of 365.242, or about 0.00274. Having a birthdate on February 29 would have a probability of 0.242 out of 365.242 or about 0.00066.
Birthdates are not randomly distributed, there is some seasonality. More children are born in the summer than in the winter (Wikipedia). Separately, studies show that childhood mortality may be dependent on birthdate. For example, death after preterm birth may be higher for babies born in the summer Epidemiology Sep 2009 and juvenile skin cancer deaths may be higher for babies born in the spring Brit J. Cancer Oct 2014.
Further, delivery date can be strongly influenced by desire of both the mother and the care giver. For instance, an obstetrician may not want to deliver a baby or make post-delivery rounds on weekends. If so, they may induce labor early in the work week. In the U.S., more babies are born on Monday through Wednesday than on Thursday through Sunday (Wikipedia). This has no effect on day of year distribution though because weekends can fall on any day. However, the desire to avoid non-work day births can affect holiday births. Many holidays are observed on Mondays, which will spread the distribution effect. However, some holidays are still observed on a specific date, including New Year’s Day, U.S. Independence Day, and Christmas. One would expect fewer births on or the days leading up to January 1.
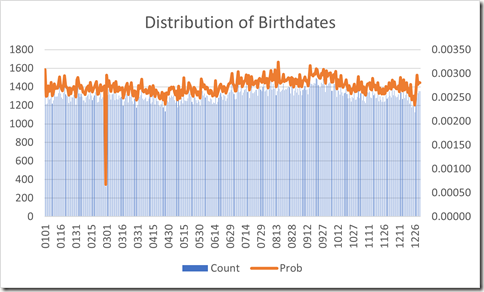
A distribution of birthdates from 480,040 life insurance policy application forms submitted between 1981 to 1994 is available at https://www.panix.com/~murphy/bdata.txt. The counts and probability are plotted in Figure 1 below.
Figure 1. Distribution of birthdates from life insurance policy applications
The dip on February 29 is expected. There is also a dip between December 22 through December 26, likely days that both pregnant patients and caregivers want to avoid spending time in a hospital.
There are 1482 birthdates listed as January 1 (p = 0.00308) which is significantly higher than expected. It is also significantly higher than the number of births on December 31 (0.00281) or January 2 (0.00252). It appears that both pregnant patients and care givers like to delivery babies on New Year’s Day. However, given a choice between a December 31 and January 1 birth, this is poor tax planning strategy (IRS).
Anyway, it isn’t that unlikely that my friend’s birthdate is actually January 1.
Here we assume that the life insurance birthdate data is accurate and truthful. That’s because people do not have much incentive to lie about their birthdate, especially since a false statement on an application can cause the company to reject a claim.
Distribution of stated birthdates
Before we conclude that my friend was born on January 1, there is a second issue. That is, why did I think that my friend’s birthdate is not January 1? Shouldn’t I believe everything people post on Facebook (Independent, Mar 2015, PLOS One Feb 2015)?
My friend’s birthdate may not be January 1 even if they say it is. Perhaps they don’t know when their actual birthdate is (they were adopted and have never seen their birth certificate) and list it as January 1 because it seems like a good default date to use. Maybe they consider their birthdate to be private information and use January 1 as their publicly stated birthdate. Perhaps they think their real birthdate is uninteresting and use January 1 to make it more interesting. Finally, maybe they just like to lie.
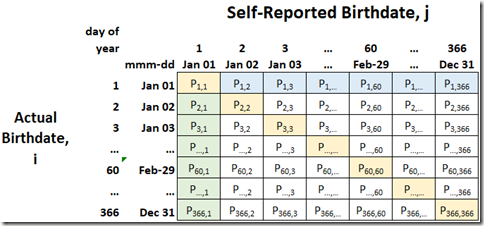
Table 1 below shows all the combinations of actual birthdates (rows) and self-reported birthdates (columns).
Table 1. Probability of all combinations of self-reported and actual birthdates
The cells are color coded. The legend is shown in Figure 2. The yellow cell in the upper left corner is the probability that a person is telling the truth; they say their birthdate is January 1 and it actually is. The green shaded cells represent people who lie. They say their birthdate is January 1, but it is not. The blue shaded cells also represent people who lie. They are born on January 1 but state their birthdate is a different date. The remaining yellow shaded cells and the white cells represent all the other combinations that do nor involve January 1.
Figure 2. Legend for Table 1
The sum of all the probabilities in the first row (yellow shaded and blue shaded cells) will give the probability that the actual birthdate is January 1. The sum for any row gives the probability the actual birthdate is the ith day of the year. We can estimate this probability using the life insurance data listed above.
The sum of all the probabilities in the first column (yellow shaded and green shaded cells) will give the probability that the self-reported birthdate is January 1. The sum for any column gives the probability a person will say their birthdate is the jth day of the year. Facebook has this data for Facebook users, but I was not able to find any reference to it.
Measuring the nonsampling error
To find the probability that my friend is telling the truth, we need to know the ratio of truth telling to lying about birthdate for everyone who claims to be born on January 1. Unfortunately, we cannot estimate it by simply combining the life insurance birthdate data with the Facebook birthdate data. The life insurance dataset and the Facebook dataset each contain 366 values. The probability matrix has 366 x 366 = 133,956 cells. Even if we make some simplifying assumptions about truth-telling vs lying, there are too many degrees of freedom in the matrix to fill it.
Conclusion
We cannot tell if my friend is telling the truth or not and do not know if their birthdate is January 1 or not. So happy birthday!
[Correction1: Changed “women” to “patients”
Correction2: Clarified that some holidays are on Monday and others on a specific date]